9. Ekologi dan Dampak Perkembangan IPTEK terhadap Kehidupan Manusia
Ekologi adalah
ilmu yang mempelajari interaksi antara organisme dengan lingkungannya dan yang
lainnya. Ekologi juga berasal dari bahasa yunani yaitu oikos (habitat) dan
logos (ilmu). Ekologi diartikan sebagai ilmu yang mempelajari baik interaksi
antara makhluk hidup maupun interaksi makhluk hidup dan lingkungannya. Istilah
ekologi pertama kali di kemukakan oleh Ernst Haeckel (1834-1914) .
Dalam ekologi makhluk
hidup dipelajari sebagai kesatuan atau sistem dengan lingkungannya. Pembahasan
ekologi tidak lepas dari pembahasan ekosistem dengan berbagai komponen
penyusunnya, yaitu faktor abiotik dan biotik.
Faktor abiotik antara lain:
- suhu
- air
- kelembaban
- cahaya
- fotografi
- manusia
- hewan
- tumbuhan
- mikroba
Perkembangan dunia iptek yang demikian pesatnya telah
membawa manfaat luar biasa bagi kemajuan peradaban umat manusia. Perkembangan
dunia iptek dianggap sebagai solusi dari permasalahan yang ada. Bahkan ada yang
memuja iptek sebagai liberator yang akan membebaskan mereka dari kurungan
kefanaan dunia.
Dampak positif dan dampak negatif dari perkembangan
teknologi dilihat dari berbagai bidang:
Bidang Informasi dan Komunikasi
Dalam
bidang informasi dan komunikasi telah terjadi kemajuan yang sangat pesat. Dari
kemajuan itu dapat kita rasakan dampak positifnya, yaitu :
- . Kita akan lebih cepat mendapatkan informasi-informasi yang akurat dan terbaru dibumi bagian manapun melalui internet.
- Kita dapat berkomunikasi dengan teman, maupun keluarga yang sangat jauh hanya dengan melalui handphone.
- Pemanfaatan jasa komunikasi oleh jaringan teroris.
- Penggunaan informasi tertentu dan situs tertentu yang terdapat di internet, biasanya disalahgunakan oleh pihak tertentu dan untuk tujuan tertentu.
2. Bidang
Ekonomi dan Industri
Dalam
bidang ekonomi teknologi berkembang sangat pesat. Dari kemajuan teknologi dapat
kita rasakan manfaat positifnya antara lain :
a. Pertumbuhan ekonomi yang semakin tinggi
b. Terjadinya industrialisasi
c. Produktifitas dunia industri semakin meningkat
3. Bidang
Sosial dan Budaya
Akibat
kemajuan teknologi bisa kita lihat :
a. Meningkatnya rasa percaya diri. Kemajuan ekonomi di
negara-negara Asia melahirkan fenomena yang menarik. Perkembangan dan kemajuan
ekonomi telah meningkatakan rasa percaya diri dan ketahanan diri sebagai suatu
bangsa akan semakin kokoh. Bangsa-bangsa Barat tidak lagi dapat melecehkan
bangsa-bangsa Asia.
b. Tekanan. Kompetensi yang tejam di berbagai kehidupan
sebagai konsekuensi globalisasi, akan melahirkan generasi yang disiplin, tekun
dan pekerja keras.
Meskipun
demikian kemajuan teknologi akan berpengaruh negatif pada aspek budaya, yaitu
akan terjadinya kemerosotan moral di kalangan warga masyarakat, khususnya
di kalangan remaja dan pelajar. Kemajuan kehidupan ekonomi yang terlalu
menekankan pada upaya pemenuhan berbagai keinginan material telah menyebabkan
sebagian warga masyarakat menjadi “kaya dalam materi tetapi miskin dalam
rohani”.
4. Bidang
Pendidikan
Teknologi
mempunyai peran yang sangat penting dalam bidang pendidikan, antara lain :
- Munculnya media massa, khususnya media elektronik sebagai sumber ilmu dan pusat pendidikan. Dampak dari hal ini adalah guru bukan satu-satu nya sumber ilmu pengetahuan.
- Munculnya metode-metode pembelajaran yang baru, yang akan memudahkan siswa dan guru dalam proses pembeljaran. Dengan kemajuan teknologi terciptalah metode-metode baru yang membuat siswa mampu memahami materi-materi yang abstrak.
5. Bidang politik
Dibidang
politik internasional juga terdapat kecenderungan tumbuh berkembangnya regionalisme.
Kemajuan di bidang teknologi komunikasi telah menghasilkan kesadaran
regionalisme. Ditambah dengan kemajuan dibidang teknologi transportasi telah
menyebabkan meningkatnya kesadaran tersebut. Kesadaran itu akan terwujud dalam
bidang kerjasama ekonomi, sehingga regionalisme melahirkan kekuatan ekonomi
baru.
Sumber:
http://nandasilfiokafia.blogspot.com/2012/06/ekologi-dan-dampak-perkembangan-iptek.html
http://id.wikipedia.org/wiki/Ekologi
http://nadiamutiaragaluh.blogspot.com/2012/05/ekologi-dan-dampak-iptek-terhadap.html
10. Himpunan dan Bilangan
- Pengertian, Penulisan dan macam himpunan
Contoh:
Umum:
·
himpunan mahasiswa Gunadarma yang
namanya mulai dari huruf A.
· ilmu geometri berhubungan dengan
matematika yang berhubungan dengan titik.
Khusus:
·
himpunan bilangan positif
·
himpunan bilangan real yang x ≤ 5004
· himpunan asli yang 2 < x < 60
MENYATAKAN ATAU
MENULIS SUATU HIMPUNAN
a) Cara
pendaftaran
Suatu cara yang dipergunakan untuk
menulis himpunan dengan cara mendaftarkan setiap elemen / unsur dari himpunan
tersebut.
Contoh :
·
himpunan bilangan bulat yang kurang
dari sama dengan 18, ditulis B= {0,1,2,3,...}
·
himpunan binatang berkaki 4, ditulis
B= {sapi,babi,anjing,...}
b) Cara pencirian
Suatu cara yang dipakai untuk
menyatakan / menulis himpuna dengan cara menulis karakteristik dari setiap
elemen / unsur himpunan tersebut.
Contoh:
· himpunan bilangan
real yang 2,005<x≤10,11
· Dinyatakan dalam bentuk pencirian
menjadi R={x/2,005<x≤10,11;xϵR}
·
himpunan bilangan bulat, dinyatakan
dalam bentuk pencirian menjadi: B={x/xϵb}
Banyaknya elemen atau unsur yang
terkandung didalam himpunan itu sendiri , biasanya di beri simbol N(A)”=
kardinal.
MACAM-MACAM
HIMPUNAN
a) Himpunan Kosong
Himpunan yang tidak memiliki elemen
atau unsur. Simbol himpunan kosong { }, Ф atau Ǿ
Contoh :
·
himpunan nama hari yang diawali
huruf
· himpunan bilangan bulat 4<x
· Jika ditulis dengan cara pencirian
menjadi : A= {x/x}
b)
Himpunan Bagian
Jika A adalah
himpunan, B juga himpunan maka himpunan A dikatakan himpunan bagian
dari himpunan B jika dan hanya jika untuk setiapn x elemen berada dalam himpunan A dan untuk setiap x elemen pula berada dalam himpunan B.
Simbol : “C”
c)
Himpunan Bagian Sejati
Jika A adalah suatu himpunan dan B
juga merupakan suatu himpunan maka himpunan A dikatakan himpunan bagian yang
sejati dari himpunan B , jika dan hanya jika untuk setiap x elemen berada dalam
himpunan B , paling sedikit sekurang kurangnyaada 1 elemen B Yang tidak berada
dalam himpunan A.
11. Relasi
Suatu relasi (biner) F dari himpunan A ke himpunan B adalah suatu
perkawanan elemen-elemen di A dengan elemen-elemen di B. didefinisikan
sebagai berikut :
Definisi: Suatu fungsi f dari himpunan A ke himpunan B adalah suatu relasi yang memasangkan setiap elemen dari A secara tunggal, dengan elemen pada B.
Definisi: Suatu fungsi f dari himpunan A ke himpunan B adalah suatu relasi yang memasangkan setiap elemen dari A secara tunggal, dengan elemen pada B.
Representasi
Relasi
Sumber: http://ilmutambah.wordpress.com/2009/08/31/pengertian-relasi-fungsi-sifat-dan-jenis-fungsi/
1. Representasi Relasi dengan Diagram
Panah
2.
Representasi Relasi dengan Tabel
3.
Representasi Relasi dengan Matriks
· Misalkan R adalah relasi dari A =
{a1, a2, …, am} dan B = {b1, b2, …, bn}.
· Relasi R dapat disajikan dengan
matriks M = [mij]
Representasi Relasi dengan Graf Berarah
· Relasi pada sebuah himpunan dapat
direpresentasikan secara grafis dengan graf berarah (directed graph atau
digraph)
· Graf berarah tidak didefinisikan
untuk merepresentasikan relasi dari suatu himpunan ke himpunan lain.
Sifat-sifat
Relasi Biner
Refleksif (reflexive)
·
Relasi R pada himpunan A disebut
refleksif jika (a, a) R untuk setiap a A.
·
Relasi R pada himpunan A tidak
refleksif jika ada a A sedemikian sehingga (a, a) R
b. Menghantar (transitive)
· Relasi R pada himpunan A disebut
menghantar jika (a, b) R dan (b, c) R, maka (a, c) R, untuk a, b, c A.
· R = {(2, 1), (3, 1), (3, 2), (4, 1),
(4, 2), (4, 3) } bersifat menghantar.
· R = {(1, 1), (2, 3), (2, 4), (4, 2)
} tidak manghantar karena.
· (2, 4) dan (4,
2) R, tetapi (2, 2) R, begitu juga (4, 2) dan (2, 3) R,
tetapi (4, 3) R.
·
Relasi R = {(1, 1), (2, 2), (3, 3),
(4, 4) } jelas menghantar
·
Relasi R = {(1, 2), (3, 4)}
menghantar karena tidak ada (a, b) R dan (b, c) R sedemikian sehingga (a,
c) R.
· Relasi yang hanya berisi satu elemen
seperti R = {(4, 5)} selalu menghantar.
Sumber: http://ilmutambah.wordpress.com/2009/08/31/pengertian-relasi-fungsi-sifat-dan-jenis-fungsi/
12. Fungsi
Untuk mendefinisikan fungsi dapat digunakan notasi berikut.
Pengertian Domain, Kodomain dan Range
Domain disebut juga dengan daerah
asal, kodomain daerah kawan sedangkan range adalah daerah hasil.
Contoh :
·
Diketahui himpunan P = { 1,2,3,4 }
dan himpunan Q = { 2,4,6,8,10,12 }
·
Relasi dari himpunan P ke himpunan Q
dinyatakan dengan "setengah dari ".
· Jika relasi tersebut dinyatakan
dengan himpunan pasangan berurutan menjadi : { (1,2),(2,4),(3,6),(4,8) }.
Domain, Kodomain dan
Range
Pada relasi
dari himpunan A ke B, himpunan A disebut Domain (daerah asal)
himpunan B disebut Kodomain (daerah kawan) dan semua
anggota B yang mendapat pasangan dari A disebut Range (derah hasil).
Contoh :
Tentukanlah domain, kodomain dan range dari relasi di bawah ini:
Jawab:
1). Domain = { 3, 5
}
Kodomain = { 1, 2, 6, 8, 9}
Range = { 1, 2, 8}
2). Domain = { 3,
5, 7, 8}
Kodomain = { 1, 2, 3, 4, 7, 8}
Range = { {1, 2, 3, 4, 7, 8}
Sumber: http://id.wikipedia.org/wiki/Fungsi_%28matematika%29
13. Proposisi
PROPOSISI
adalah “pernyataan dalam bentuk kalimat yang memiliki arti penuh, serta mempunyai nilai benar atau salah, dan tidak boleh kedua-duanya”.
Maksud kedua-duanya ini adalah dalam suatu kalimat proposisi standar tidak boleh mengandung 2 pernyataan benar dan salah sekaligus.
Rumus ketentuannya :
Q + S + K + P
Keterangan :
Q : Pembilang / Jumlah
(ex: sebuah, sesuatu, beberapa, semua, sebagian, salah satu, bilangan satu s.d. tak terhingga)
Q boleh tidak ditulis , jika S (subjek) merupakan nama dan subjek yang pembilang nya sudah jelas berapa jumlahnya :
a. Nama (Pram, Endah, Ken, Missell, dll)
b. Singkatan (PBB, IMF, NATO, RCTI, ITC, NASA, dll)
c. Institusi (DPRD, Presiden RI, Menteri Keuangan RI, Trans TV, Bank Mega, Alfamart, Sampurna, Garuda Airways, dll)
S : Subjek adalah sebuah kata atau rangkaian beberapa kata untuk diterangkan atau kalimat yang dapat berdiri sendiri (tidak menggantung).
K : Kopula, ada 5 macam : Adalah, ialah, yaitu, itu, merupakan.
P : Kata benda (tidak boleh kata sifat, kata keterangan, kata kerja).
Contoh :
1. Gedung MPR terletak 500 meter dari jembatan Semanggi.
Jawaban :
1. Cari P (kata bendanya dulu) : Gedung MPR atau Jembatan Semanggi,
2. Pasang K (kopula) yang cocok : adalah
3. Bentuk S (subjek) yang relevan : (lihat contoh)
4. Cari bentuk Q – nya yang sesuai.
Benar :
Sebuah + gedung yang terletak 500 meter dari jembatan Semanggi + adalah + gedung MPR.
Salah
500 meter + dari jembatan Semanggi + adalah + gedung MPR.
adalah “pernyataan dalam bentuk kalimat yang memiliki arti penuh, serta mempunyai nilai benar atau salah, dan tidak boleh kedua-duanya”.
Maksud kedua-duanya ini adalah dalam suatu kalimat proposisi standar tidak boleh mengandung 2 pernyataan benar dan salah sekaligus.
Rumus ketentuannya :
Q + S + K + P
Keterangan :
Q : Pembilang / Jumlah
(ex: sebuah, sesuatu, beberapa, semua, sebagian, salah satu, bilangan satu s.d. tak terhingga)
Q boleh tidak ditulis , jika S (subjek) merupakan nama dan subjek yang pembilang nya sudah jelas berapa jumlahnya :
a. Nama (Pram, Endah, Ken, Missell, dll)
b. Singkatan (PBB, IMF, NATO, RCTI, ITC, NASA, dll)
c. Institusi (DPRD, Presiden RI, Menteri Keuangan RI, Trans TV, Bank Mega, Alfamart, Sampurna, Garuda Airways, dll)
S : Subjek adalah sebuah kata atau rangkaian beberapa kata untuk diterangkan atau kalimat yang dapat berdiri sendiri (tidak menggantung).
K : Kopula, ada 5 macam : Adalah, ialah, yaitu, itu, merupakan.
P : Kata benda (tidak boleh kata sifat, kata keterangan, kata kerja).
Contoh :
1. Gedung MPR terletak 500 meter dari jembatan Semanggi.
Jawaban :
1. Cari P (kata bendanya dulu) : Gedung MPR atau Jembatan Semanggi,
2. Pasang K (kopula) yang cocok : adalah
3. Bentuk S (subjek) yang relevan : (lihat contoh)
4. Cari bentuk Q – nya yang sesuai.
Benar :
Sebuah + gedung yang terletak 500 meter dari jembatan Semanggi + adalah + gedung MPR.
Salah
500 meter + dari jembatan Semanggi + adalah + gedung MPR.
KOMBINASI PROPOSISI
Satu atau lebih proposisi dapat
dikombinasikan untuk menghasilkan proposisi baru. Operator yang digunakan untuk
mengkombinasikan proposisi disebut operator logika. Operator logika dasar yang
digunakan adalah dan (and), atau (or),
dan tidak (not). Proposisi baru yang diperoleh dari
pengkombinasian tersebut dinamakan proposisi majemuk (compound
proposition). Dalam logika, dikenal 5 buah operator seperti dijelaskan
dalam tabel berikut ini.
Simbol
|
Arti
|
Bentuk
|
-
|
Tidak / Not / Negasi
|
tidak…
|
∧
|
Dan / And / Konjungsi
|
…dan…
|
∨
|
Atau / Or / Disjungsi
|
…atau…
|
⇒
|
Implikasi
|
Jika…maka…
|
⇔
|
Biimplikasi
|
…jika dan hanya jika…
|
Contoh:
p : Hari ini hujan deras.
q : Mahasiswa tidak kuliah.
Maka:
p ∧
q : Hari ini hujan deras dan mahasiswa tidak kuliah.
p ∨ q
: Hari ini hujan deras atau mahasiswa tidak kuliah.
-p
: Hari ini tidak hujan deras.
p ∧ -q :
Hari ini hujan deras dan mahasiswa kuliah.
-(-p) : Tidak benar bahwa hari
ini tidak hujan deras.
p ⇒ q
: Jika hari ini hujan deras, maka mahasiswa tidak kuliah.
p ⇔ q :
Hari ini hujan deras jika hanya jika mahasiswa tidak kuliah.
HUKUM LOGIKA PROPOSISI
Berikut adalah hukum-hukum logika
yang berlaku pada proposisi.
1. Hukum Identitas
p ∨ F ⇔ p
p ∧ T ⇔ P
2. Hukum Null / dominasi
p ∧ F ⇔ F
p ∨ T ⇔ T
3. Hukum Negasi
p ∨ -p ⇔ T
p ∧ -p ⇔ F
4. Hukum Idempotent
p ∨ p ⇔ p
p ∧ p ⇔ p
5. Hukum Involusi (negasi ganda)
-(-p) ⇔ p
6. Hukum Penyerapan (absorpsi)
p ∨ ( p ∧ q) ⇔ p
p ∧ (p ∨ q) ⇔ p
7. Hukum Komutatif
p ∨ q ⇔ q ∨ p
p ∧ q ⇔ q ∧ p
8. Hukum Asosiatif
p ∨ (q ∨ r) ⇔ (p ∨ q) ∨ r
p ∧ (q ∧ r) ⇔ (p ∧ q) ∧ r
9. Hukum Distributif
p ∨ (q ∧ r) ⇔ (p ∨ q) ∧ (p ∨ r)
p ∧ (q ∨ r) ⇔ (p ∧ q) ∨ (p ∧ r)
10. Hukum De Morgan
- (p ∧ q) ⇔ -p ∨ -q
- (p ∨ q) ⇔ -p ∧ -q
TABEL KEBENARAN
Tabel kebenaran
adalah suatu tabel yang memuat nilai kebenaran proposisi majemuk. Nilai
kebenaran dari proposisi majemuk ditentukan oleh nilai kebenaran
proposisi-proposisi pembangunnya. Jika kalimat majemuk yang akan kita buat
tabel kebenarannya memuat n proposisi tunggal, maka jumlah komposisi nilai
kebenarannya ada 2n. Berikut ini adalah tabel kebenaran dari operator-operator
logika dasar.
P
|
Q
|
-P
|
-Q
|
p ∨ q
|
p ∧ q
|
p ⇒ q
|
p ⇔ q
|
T
|
T
|
F
|
F
|
T
|
T
|
T
|
T
|
T
|
F
|
F
|
T
|
T
|
F
|
F
|
F
|
F
|
T
|
T
|
F
|
T
|
F
|
T
|
F
|
F
|
F
|
T
|
T
|
F
|
F
|
T
|
T
|
Note :
T : True
F : False
Sumber: http://andriksupriadi.wordpress.com/2010/04/01/pengertian-proposisi/
14. Logika
Logika Matematika adalah cabang ilmu
di bidang matematika yang memperdalam masalah logika. Yang memperjelas logika
dengan kaidah-kaidah (aturan) matematika.
Trend perkembangan:
1.
Logika Proporsional
Logika Proporsional adalah Logika yang memproses
penarikan kesimpulan secara logis (logical derivation) dari
proposisi-proposisi.
Contoh: Program komputer ini mempunyai bug. Proposisi atau
pernyataan ada yang berbentuk :
· Atomik (atomic proposition) :
proposisi yang tak dapat dipecah menjadi beberapa proposisi.
Contoh : Anda
harus belajar dengan rajin.
· Majemuk (compound proposition):
gabungan dari beberapa proposisi atomik menggunakan perangkai (connectives).
Contoh : Anda harus belajar dengan
rajin atau Anda akan gagal ujian.
2. Bukan Proposisi
Pernyataan bukan proposisi adalah Pernyataan
yang menimbulkan banyak pendapat. Misal :
·
Angka 13 adalah angka sial.
·
Angka 7 adalah angka keberuntungan.
·
Ungu adalah warna janda.
·
Kalimat perintah dan kalimat tanya.
·
Badu, kerjakan tugas tersebut!
Sebuah proposisi tidak
boleh digantikan oleh proposisi lain meski memiliki makna sama. Contoh :
·
A = Badu lapar.
·
B = Badu kenyang.
·
Bagaimanakah bentuk pernyataan
“Tidak A”??
·
Bolehkah “Tidak A” digantikan oleh
B??
3. Variabel
Proporsional
Penggunaan huruf latin
sebagai variabel proposisional, tanpa menghilangkan sifat utama proposisi.
Contoh:
·
A = Badu lapar.
·
B = Badu kenyang.
Huruf latin yang tidak boleh
digunakan: T dan F --> konstanta proporsional.
Sumber: http://alfisyahrinuzula.blogspot.com/2013/11/pengantar-logika-matematika.html
NAMA : D.PUSPA PANE
NPM : 11513976
KELAS : 1PA10
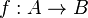



Tidak ada komentar:
Posting Komentar